接触网荷载和应力的假设

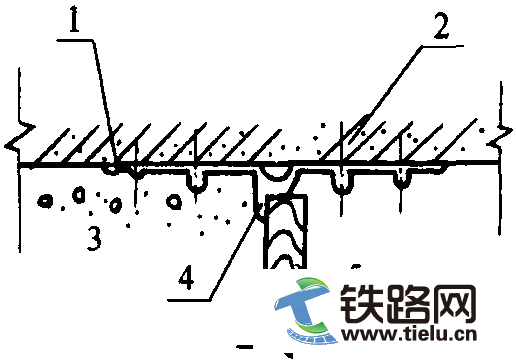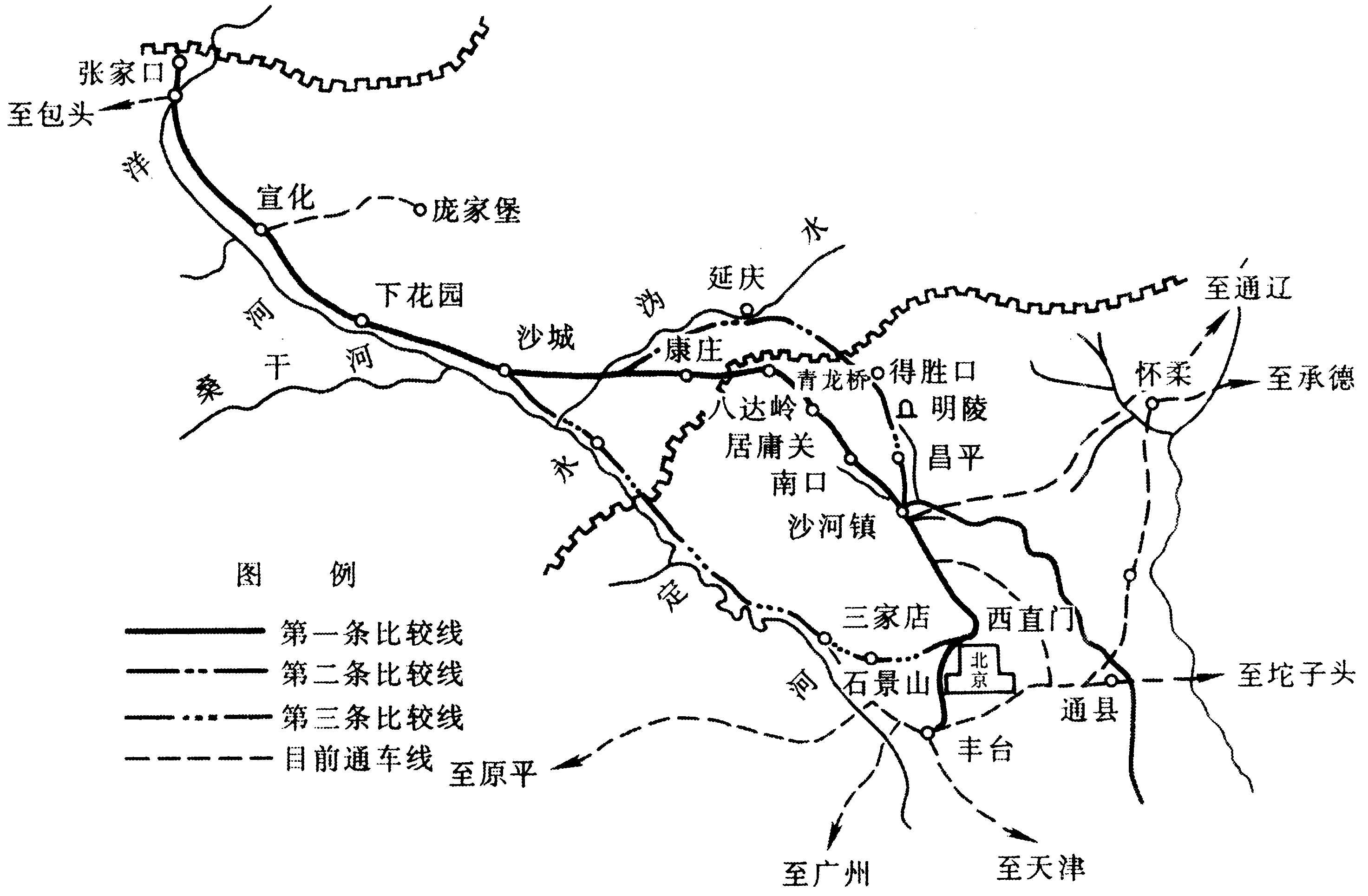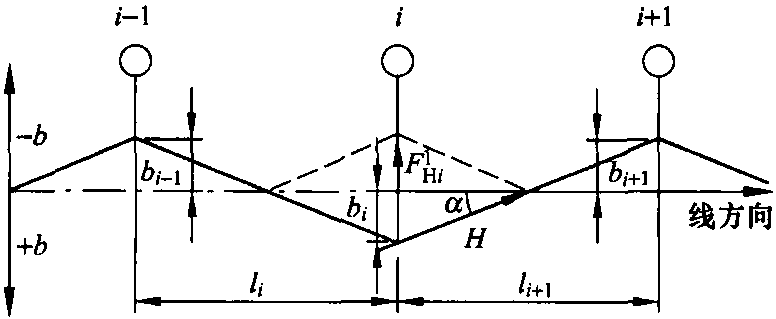
图5.2 由于线索交替横向位移 (拉出值) b产生的作用于导线的张力H之水平分力

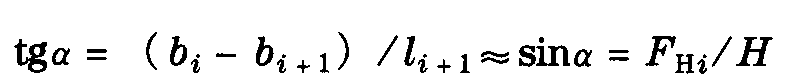
角度较小时，tgα≈sinα，例如对于∠α=10°来说，误差是15%

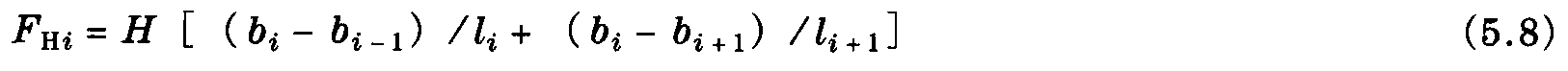
F_Hi力是作用在导线上的张力的水平分力，把导线从线路中心线拉出。当b_i＝b、b_i-1＝b_i+1＝-b和l_i+1＝l_i＝l时，在沿直线情况下，公式可以简化为

举例： 德国铁路的标准架空接触网结构中，最大时速200km以下时，取b=0.4m和H=10kN，支柱间距离设为75m，可计算出导线张力的水平分力为213.3N，相当于2.1%。

固定锚固或张力自动补偿

象前面那样，采用相同的近似值，因横向位移 “Z”值至锚固点或补偿装置方向产生的水平分力 (如图5.3所示) 是

图5.3 由于下锚方向或补偿装置而产生的导线张力的水平分力

F_H＝Hsinα≈Htgα

所以，相对应地

如果所有的l值相等，所有的“Z”值也相等，而半个支柱宽度忽略不计，则方程可简化为

沿着无超高水平轨道，距离Z=半个支柱宽度+MFE，(MFE是支柱前缘和线路中心线之间的距离)。在下面的表达中，支柱号为i的MFE尺寸指定为l_Ai，对于中心锚结柱，可采用下面这个公式

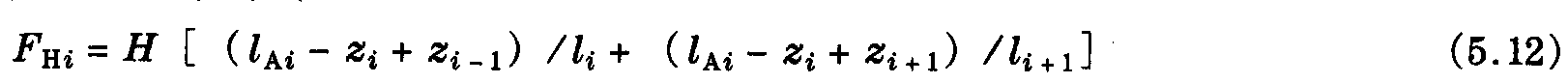
如果“Z”距离相等并且支柱间距均等，可以简化为

F_H＝2H (l_A+半支柱宽度)/l (5.13)

举例： 如图5.4所示中心锚柱，距离lA≈4m，柱间距为65m，水平作用在锚固绳上的接触线张力为10kN，则可计算得出与中心线成直角作用的水平分力是1.23kN。

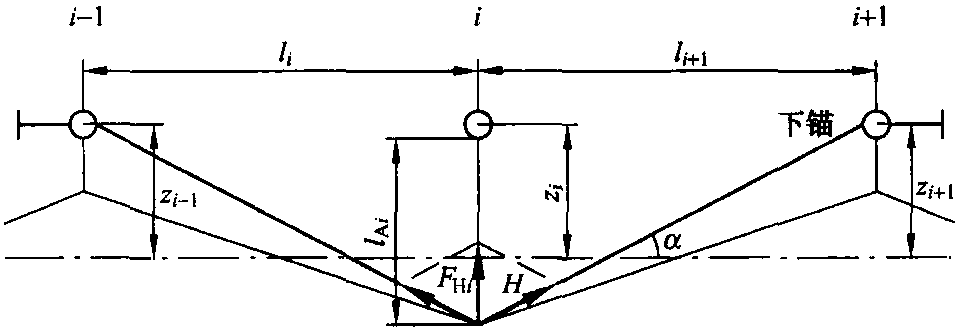
图5.4 由于横向下锚位移产生的作用于中心锚柱上的水平分力

曲线线路

在曲线上，由于导线沿曲线拉出，拉出值和锚固力的缘故产生了作用于架空接触网导线的水平分力。

从图5.5，对于曲线半径为R的曲线线路，可推导出下式

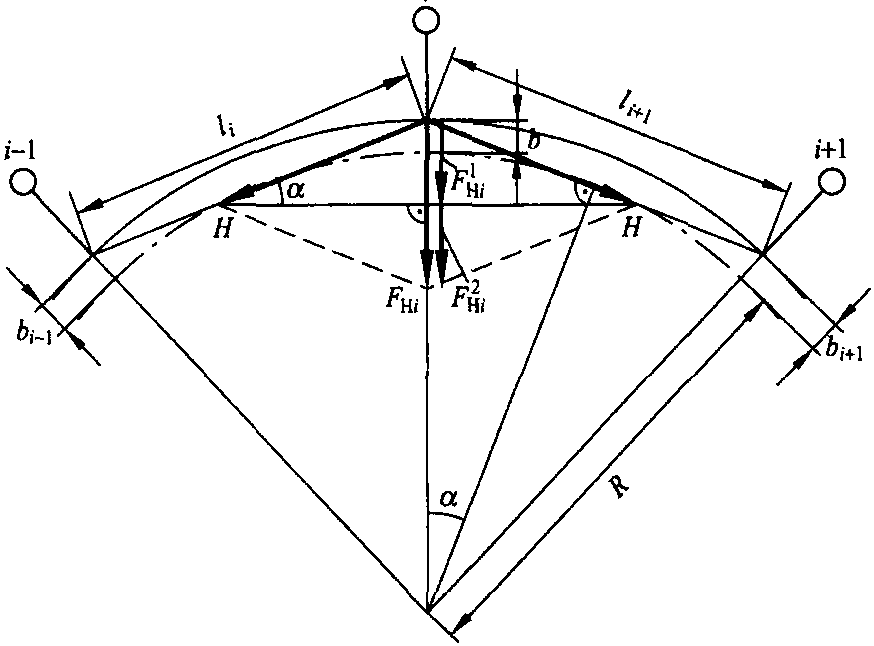
图5.5 曲线上导线张力的水平分力

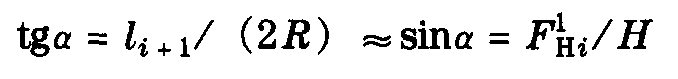
曲线正定位力(通常也称为径向荷载) 是相邻两跨距导线张力的水平分力之和

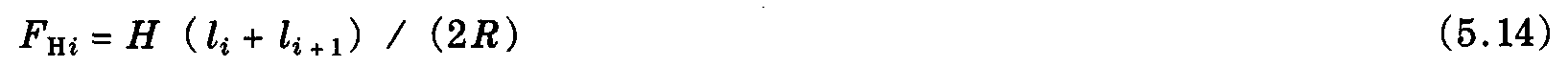
对于等距跨距，可简化为