接触网荷载和应力的假设

考虑到附加的水平偏移，又进一步增加了分力

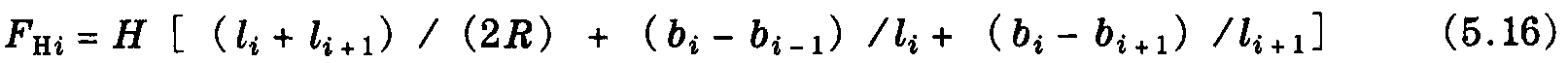
在锚杆处，根据式 (5.12) 和式 (5.14)，对于曲线正定位可得

(5.17)

对于接触线和承力索自动补偿的中心柱

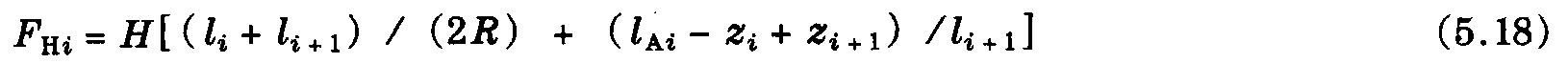
线索和导线由于温度变化造成长度改变，它使得拉出值和相关水平分力发生变化。如图5.6所示，承力索和接触线的膨胀和收缩变量值△L造成拉出值变化△b，代入公式

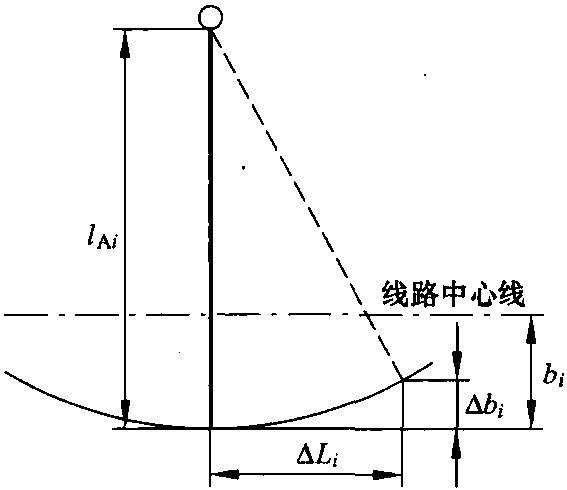
图5.6 在热膨胀或收缩△L_i情况下，长l_Ai腕臂的位置变化造成接触线横向位移的变化△b

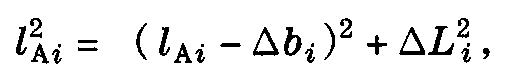拉出值变化的近似值(忽略△b_i的平方项)为

复位力(也称为腕臂阻力)

由于腕臂位置的变化，△L_i产生了曲线或拉出力，拉出力围绕腕臂轴向运动产生了力矩。该力矩被接触线力的水平分力之差形成的力矩所抵消。这个差称之为复位力，水平张力的另一部分传递给了支柱。

对于小的角度，允许用近似值tgα≈sinα来计算复位力，如图5.7，得出公式

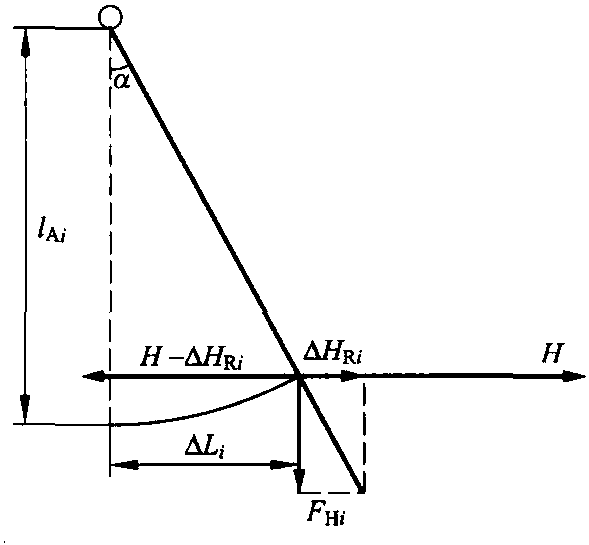
图5.7 由于位置变化△L_i作用在长l_Ai腕臂上的复位力△HR_i

相对于承力索，lA是支柱的线路侧面到承力索线夹中心的距离，半个补偿长度 (锚段长度) 内的复位力之和不能大于 (0.07～0.08) ×H [5.4]。如果温度骤降，由于复位力加上距离补偿装置间距的增加使得接触线的张力增大。如果温度升高，接触线张力则相应下降。当进行接触网设计时，确保中心锚结两侧的接触线和承力索张力尽可能相等是很重要的。在半个补偿段内，每个支持装置上的复位力可以用式 (5.20) 计算得出。中心点附近处的最大接触线张力变化是需要注意的，可以用复位力的和来表示。

对于中心锚结前的最后一个跨，接触线纵向力的总变化为

在直线上，根据式 (5.8) 作用于各套支持装置上的复位力是接触线和/或承力索拉出值引起的。然而，由于横向力沿着直线从一个支持装置到下一个支持装置的作用是反方向的，复位力实际上被相互抵消了，可以采用式 (5.20) 来计算各个复位力。

在曲线上，R、l和l_A是常数，复位力用式 (5.14)、式 (5.20) 计算并代入△L_i=ilα△， 可得出

中心锚结前的最后一个跨，中心位置处的水平张力差是