5.2.1 电车型简单悬挂接触网

5.2.1.1 等高悬挂

本节讨论的是在接触线自动补偿控制状态下，即承受恒定张力时 (单位长度特定荷载下) 的导线弛度; 第5.3节讨论的是两终端固定锚固中因过载或温度变化引起的张力变化。

讨论的第1种情况是支持装置上等高悬挂的两根导线 ，S是沿导线作用的张力。S的垂直分力为V，水平分力为H，因为在接触网设施中对接触线和导线的弯曲强度的要求相对较低，因此只考虑沿这些导线作用的张力。假设导线在支持装置处装有一个轴且被固定以防止其纵向移动。按照图5.8所示，作用在长度△L线段上的力平衡为

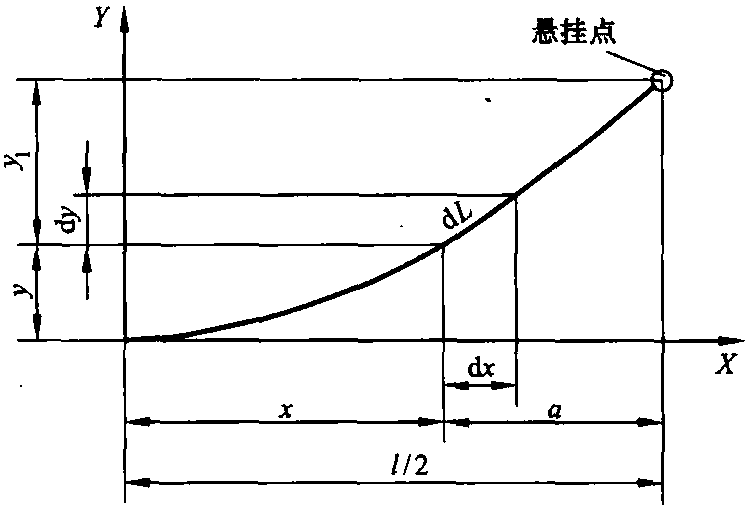
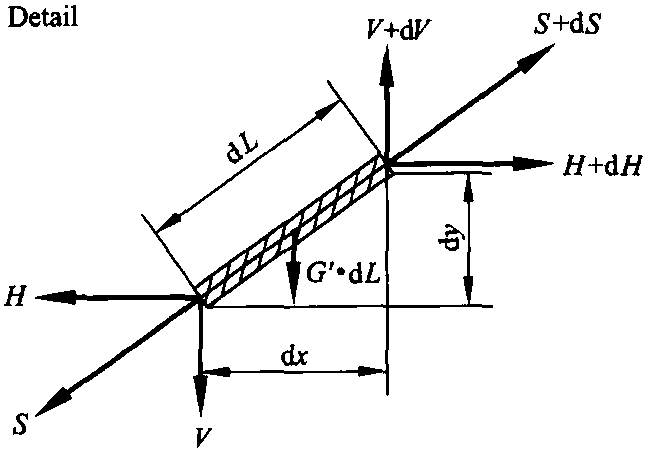
图5.8 单根架空线弛度

—对于水平力

H+dH-H=0，→dH=0

这里，通过积分H=常数;

—对于垂直力

V+dV-V-G′dL=0，→dV= G′dL

用和关系式dy/dx=V/H(由图5.8中推导出)，可以找出弛度曲线的微分方程为

这个答案通常是条悬垂曲线

如 [5.7] 所述，把式 (5. 31) 代入到微分方程式 (5.30) 中可以进行验证。

然而，在架空接触网中，线L比支柱间距l仅长0.5‰～1‰，因此，可以认为dL≈dx是正确的，线弛度的微分方程可简化为

解式是抛物线方程

如图5.8，对应悬挂点的弛度y1，在与悬挂点的距离为a的任意一点，其弛度为

比较一下，弛度值y1，是跨距中心点x的函数，可以得出：

当a=1/2或x=0时，弛度最大，公式等于

在与悬挂点距离为a的弛度y1也可用最大弛度fmax来表示如下

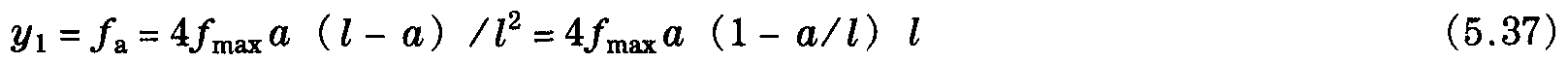
举例： CuAC-100型接触线l =40m、承受恒定张力10kN，其最大弛度为

吊弦间距为12m的链型架空接触网中，两个吊弦之间的同一接触线弛度约为16mm。

5.2.1.2 不等高悬挂

如果导线的两个相邻悬挂点的高度差是h，可以采用图5.9的尺寸和两个部分纵向跨距l1和l2，以及关系式l=0.5 (l1+l2) 和h=f1-f2

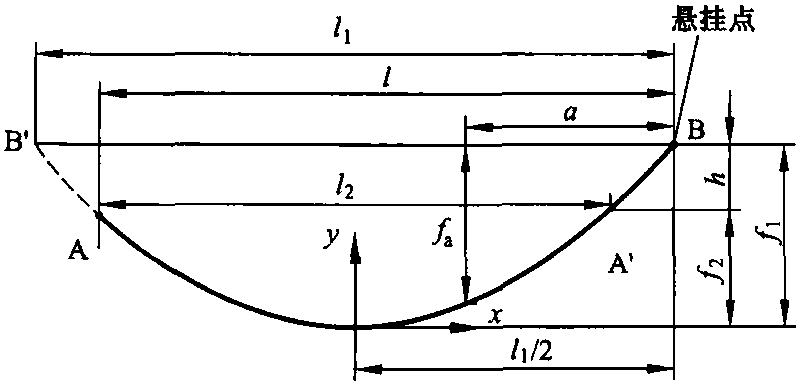
图5.9 不等高悬挂的导线弛度