接触网的物理状态变换方程式

²铝加强线和用作并行馈线或旁路线来说，可使用表5.8中给出的值。　表中所给的值 [根据式 (5.54) 计算] 可用于第6.11.5节中作为验证供电线满足绝缘间隙要求的基础！

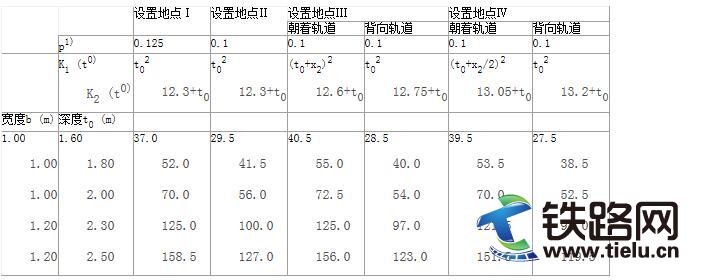
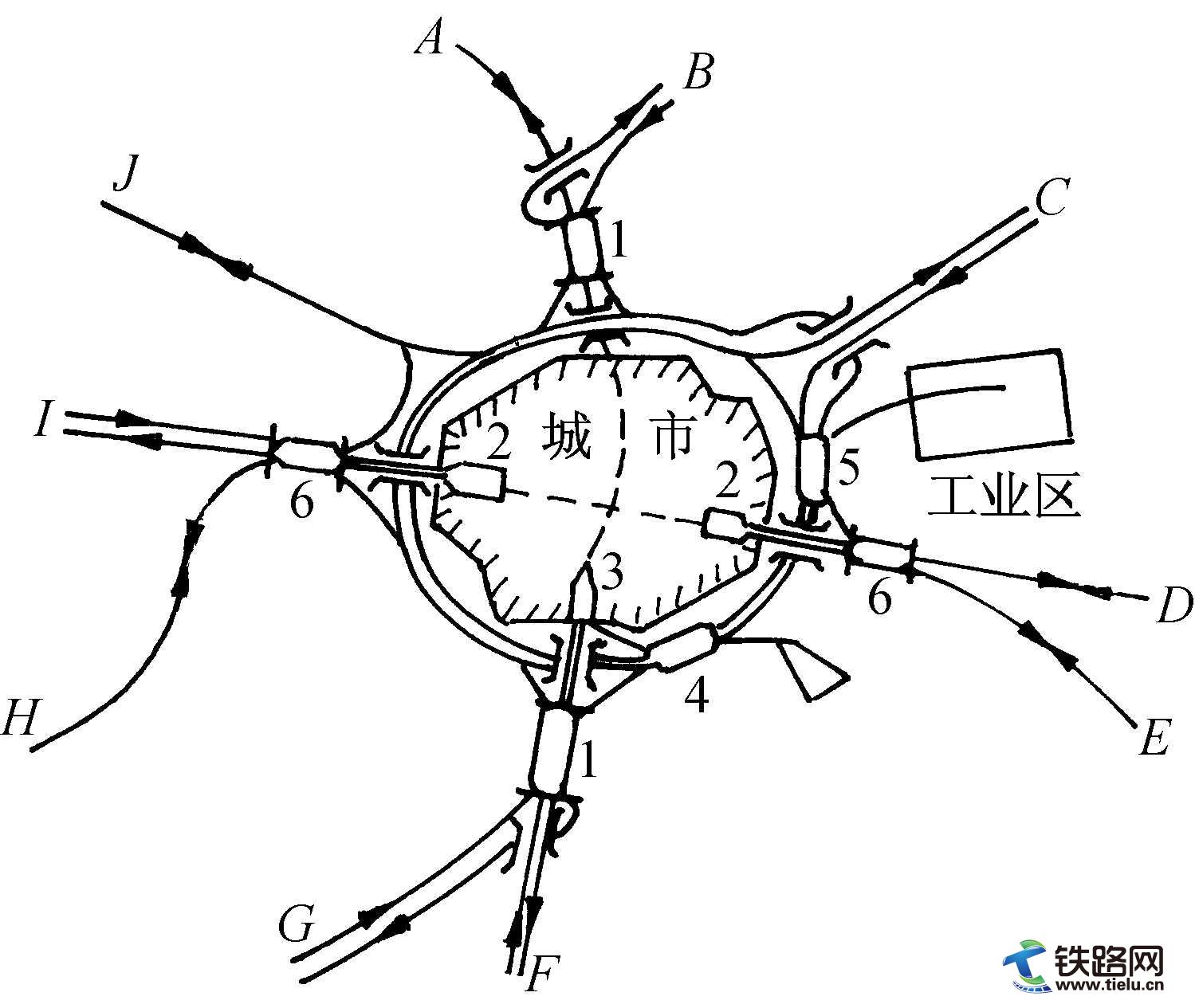
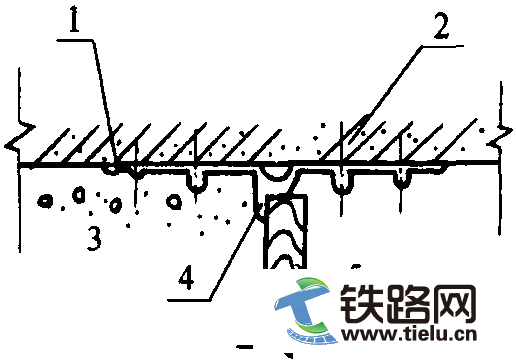
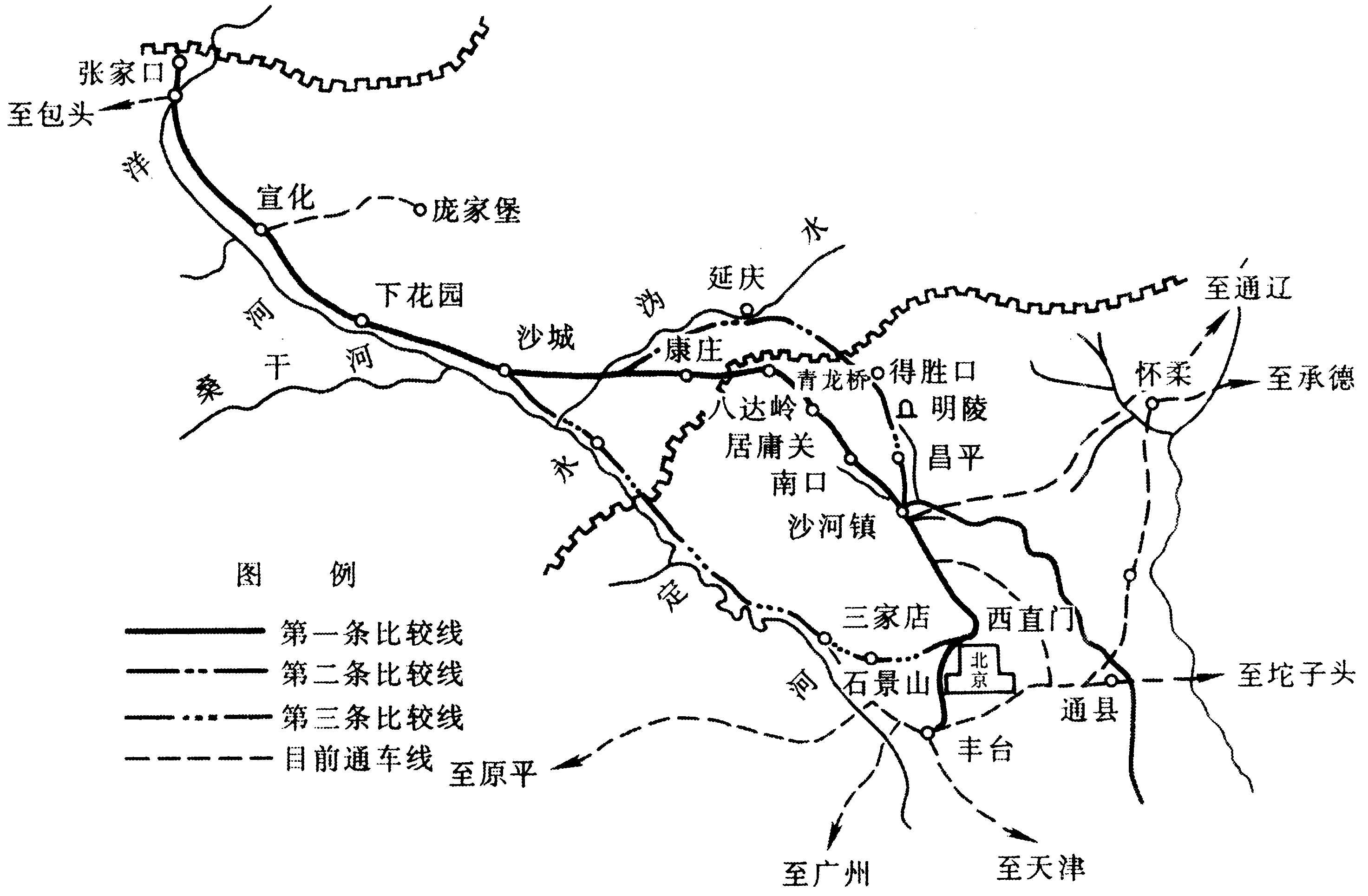
表5.8 温度变化情况下，240mm²铝导线在无自动补偿状态下的弛度和拉伸应力

注 1)根据式 (5.28)，相应冰荷载7.03 N/m; 最大拉伸应力极限值20N/mm²。

可以用电车型接触网的无补偿接触线来说明式 (5.54)的应用。实际应用中可转换式(5.54) 求出要求的张力参数Hx，为

对于不同长度l_i的n个跨距的锚段长度，可以替换为 [5.7] 所述的理想的或当量跨距

举例： 确定在-20℃温度下的10跨区段且当量跨距为45m的电车型接触网的张力，该接触网由CuAC-100型接触线组成，安装温度为+10℃、张力为8kN。根据表5.1和表2.11： A=100mm²; E=124kN/mm²; α=17×10^-6K^-1; G'₀＝G′_x＝8.73N/m。把这些值和温度代入式 (5.55) 中可以得出

还原简化为

H_x²(H_x-13078N) =79.74·10⁹N³

这个H_x的三次方程式可以用迭代法解出：

H_x＝14000N得出H_x²(H_x-13078N)=180×10⁹N³

H_x＝13500N得出H_x²(H_x-13078N)=76.9×10⁹N³

H_x＝13550N得出H_x²(H_x-13078N)=86.7×10⁹N³

H_x＝13515N得出H_x²(H_x-13078N)=79.8×10⁹N³

因此温度在-20℃时，张力是13515N。温度升到+40℃时，张力降到4452N。在-20℃时，相对应的弛度值是0.16m，而+40℃时弛度值是0.50，两者差为0.34m。

这个例子说明了终端为硬锚的接触线的张力变化大。随着支柱跨距的减小，张力的变化增大。总的锚段长度对这种现象没有影响。因此可以安装弹簧来减小张力的变化，弹簧的伸长为

这里，c_CW是弹簧常数。各种因数累加之和引起了长度变化，这样的话整个变量式可以表示为

L_x-L₀＝△L_W+△L_E+△L_CW

使用式 (5.48)、式 (5.49)、式 (5.53) 和式 (5.57)，可以得出一个与式 (5.55) 类似的状态公式，该公式用于弹簧补偿的锚段的计算

(5.58)

举例：如前例所述，锚段内安装常数为c_CW＝10kN/m的弹簧，在温度-20℃时，可以用H_x三次方程式计算得出张力9566N。温度-40℃时，计算出张力为6050N。从这里很明显看出，安装的弹簧减少了拉伸力和弛度的变化。

在承力索采用硬锚的半补偿接触网中，式 (5.54) 是确定承力索拉伸应力和弛度的基础！按照式 (5.8)，下面这个公式用于在给定x状态下的最大承力索弛度的计算

冰载情况下，预期温度-5℃左右，必须考虑G′_OHLx＝G′_OHL+ G′_ice

就其他一切情况而言，G′_OHLx＝ G′_OHL0＝G′_CA+G′_CW

如果f_Tmax值规定有极限，0状态下承力索的张力H′C_A0必须通过数字方式求解上式来确定。