接触网的风偏移计算

当b_i＝b_i+1＝-b时，考虑“+”、“-”符号，得出下式

5.4.3 架空接触悬挂的风偏移

如果式 (5.64)、式 (5.65)、式 (5.68) 分别用于承力索或接触线的话，由于不同的风力和张力作用得出的横向偏移也会不同。当承力索或接触线在风力作用下偏移不同时，由于彼此之间通过吊弦连接，它们会互相施加以力。

到目前为止，我们在实际计算时忽略了这种情况，架空接触网悬挂偏移的计算是基于这样的假设，即整个接触悬挂受风影响时的偏移相同，风作用力的计算针对的是整个架空接触网的接触悬挂。它在相应的公式中使用并把承力索和接触线张力之和作为张力考虑，见式 (5.67) 和式 (5.71)。根据实际的参数和状况，这种方法推导出的偏移值结果可能比实际值高或低。

如果认为风载下接触线和承力索的偏移不同，吊弦受拉产生位置倾斜并且把一部分风载传给低偏移的元件。下一章介绍了基于 [5.9] 的方法，这种方法认为沿整个跨距上，接触线和承力索通过吊弦相互作用。由于风力作用，接触线和承力索之间作用的力呈线性力分布状态，也就是说单位长度的力定为F′_W，CWCA。因为是近似值，沿跨距的吊弦长度假设都是等于特定的平均值。这就意味着，如图5.13中看到的那样，跨距内所有的吊弦有着相同的垂直于铁路线的线平面偏移角。这个假设方法适合接触悬挂的结构高度大于1.4m的情况。

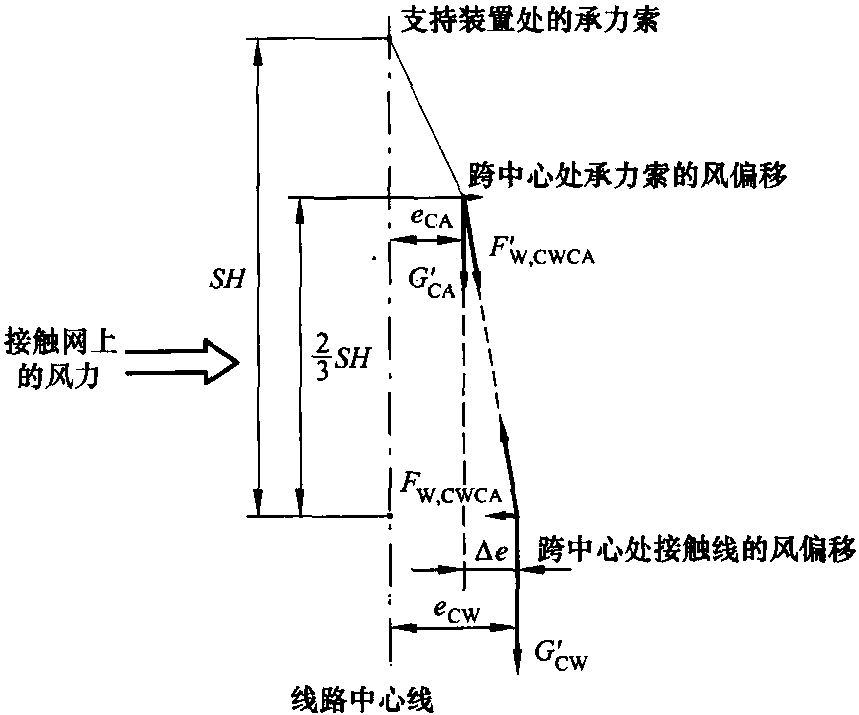
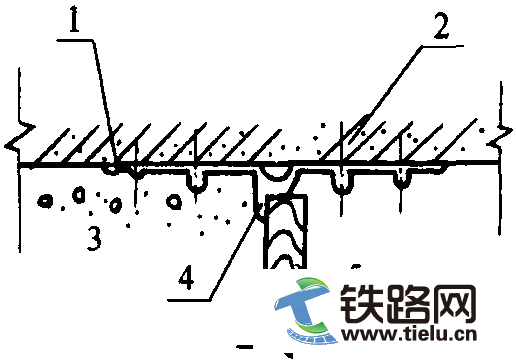
图5.13 接触线偏移比承力索大，吊弦传递耦合力到承力索情况下的架空接触网设备倾斜偏移

用一个抛物线函数来表示由于接触线施加单位长度力F′_W，CWCA而产生的承力索水平偏移。用图5.14所示的半个跨距来表达，得出

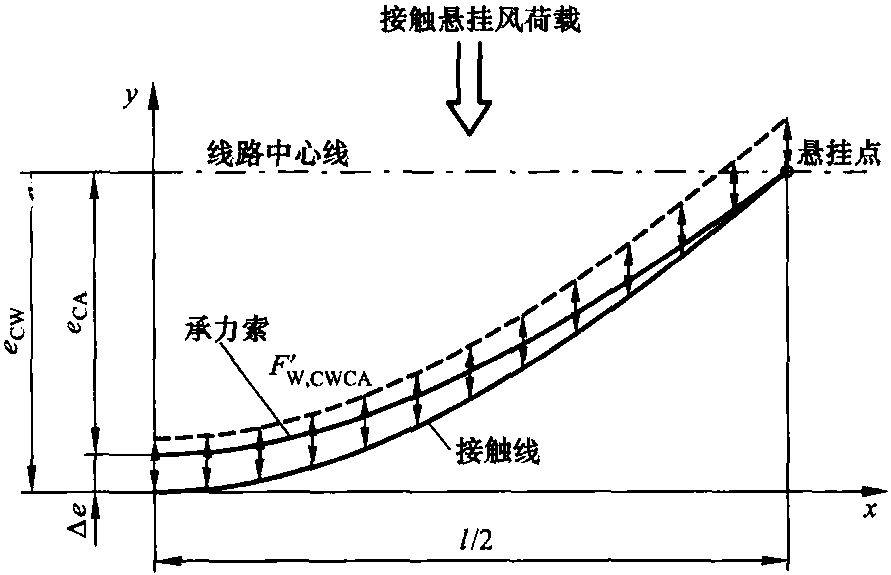
图5.14 风载作用下，通过承力索和接触线间吊弦起作用的耦合力的分力F'_W，CWCA

计算风载下接触线和承力索的完全偏移，必须考虑下面单位长度的荷载：

—承力索

—接触线

在这些讨论中，已经假设在承力索张力和接触线张力相等的情况下，接触线的偏移要比承力索的偏移大，因为前者的线径要大些。这种情况下，承力索减小了接触线的风偏移。式 (5.80) 中没有考虑接触线拉出值。在跨中处，接触线和承力索的不同偏移产生的横向偏移差定义为△e，它用下式计算

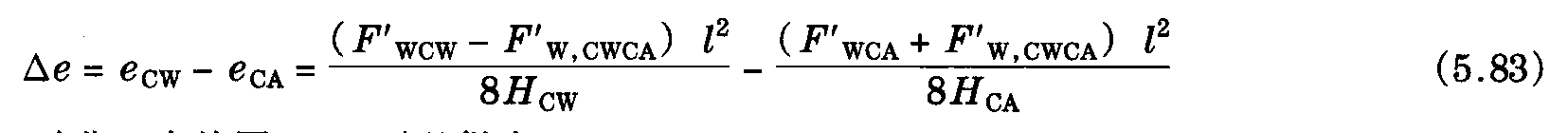
更进一步从图5.13可以得出

这里，SH是结构高度，解题可得出△e

通过式(5.83) 等于式(5.84)，可以得出与长度相关的风载下接触线和承力索相互作用力的公式

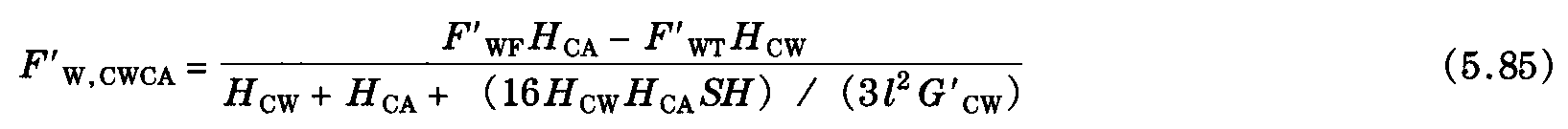
采用有限元分析(FEA) 方法使用计算机程序对架空接触网的接触悬挂偏移进行精确和现实的计算是可以做到的。用几个例子来说明FEA的应用。图5.15示出采用FEA方法确定的Re200型标准架空接触网的接触悬挂中 (支柱间距为80m) 接触线和承力索的相对位置。