接触网的纵向跨距和锚段长度

—最大速度时受电弓弓头的工作范围; a₂—速度较低时受电弓弓头的工作范围; a₃—风载下接触线允许的位置范围; d—最大速度时受电弓弓头位置; e—速度较低时受电弓弓头位置; f—最大速度时受电弓弓头的横向位移

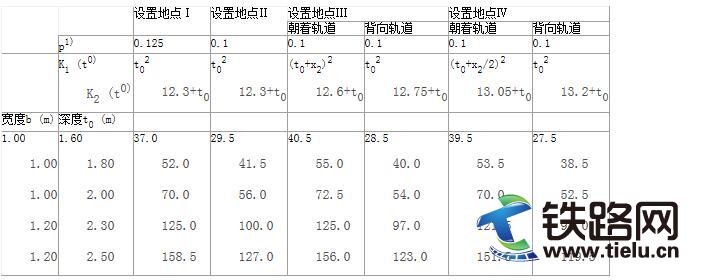
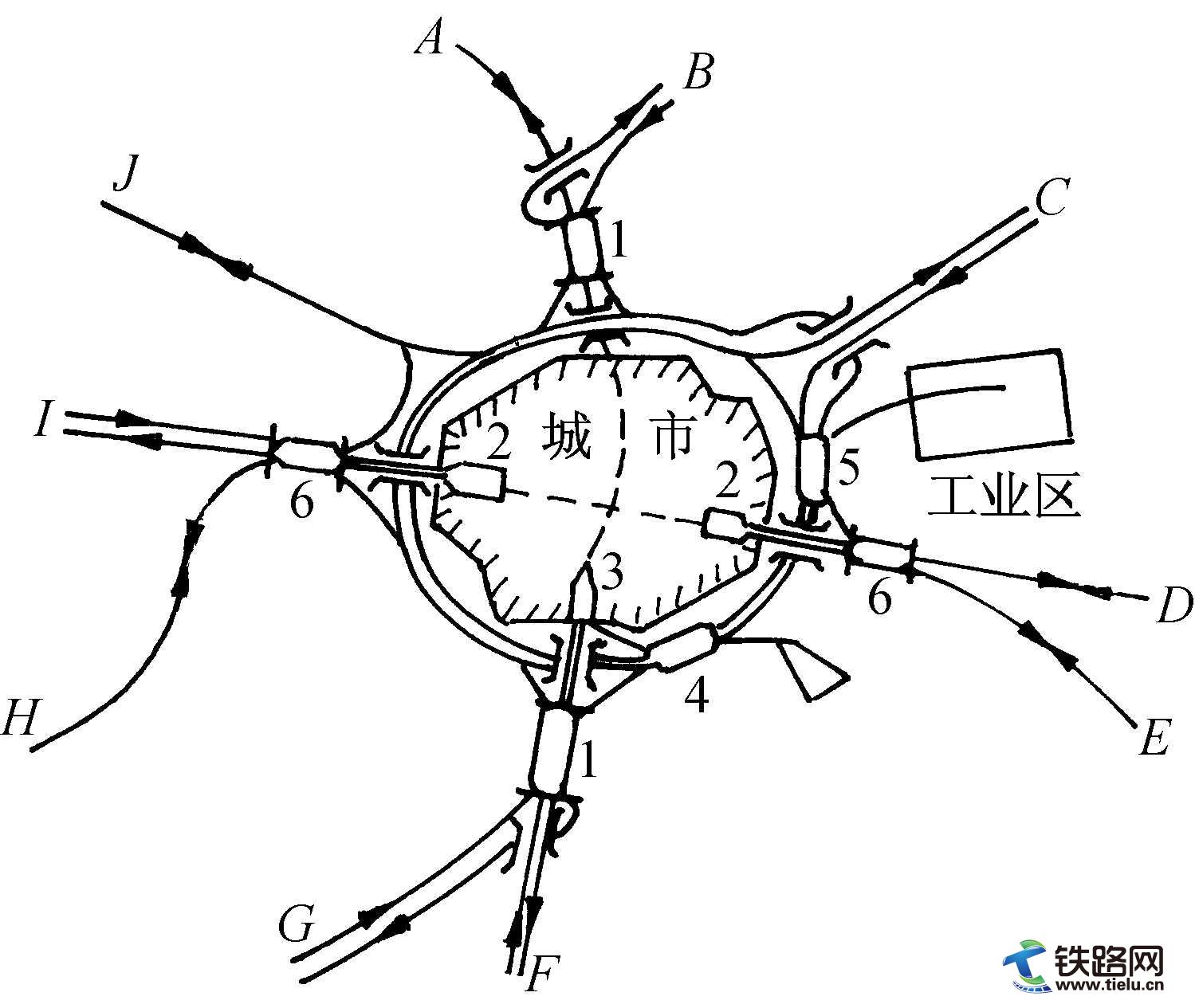
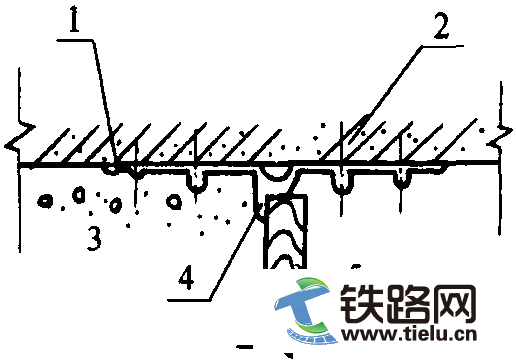
无风情况下，接触线应在滑板的范围内与受电弓弓头相接触。德国铁路采用标准受电弓设计，受电弓滑板是1030mm长。因此支持装置处的拉出值被限定为±400mm。支持装置处完全采用最大位移是不可能的 (理论上使用受电弓头的整个工作范围是可行的)。在曲线外侧，接触线位置最大达515mm是允许的; 在曲线内侧，图5.18示出允许采用的与曲线半径相关的数值。这些数值是依照图5.17从受电弓横向摆动中推算出来的。

德国铁路设计架空接触网时，如图5.18所示，采用的是接触线与曲线半径相关的位置极限值。图5.18中的数据基于德国铁路标准9 Ebs 02.05.06。如果接触线在跨中心处的线路中心线上时，那么位移相当于接触线的风偏移，也就是说，接触线在该点距线路中心线的c值为0。在其他情况时，接触线的位置极限值是c值和风偏移的和。图5.19说明了这些因数的相互关系。

法国国铁规定用于所有曲线半径的极限位置均为350mm，它与德国铁路相比，适用于有效宽度更短些的受电弓弓头。

5.5.2.5 纵向跨距的确定

风力产生的导线位移是架空接触网中确定纵向跨距的决定性因数，如果风作用下接触线允许的位置极限值为已知，可以用第5.4节中所示公式作为计算最大可能纵向跨距的根据。

在直线上，按图5.11说明和式 (5.64) (b_i+1＝ -b₂时，b_i＝ b₁) 可以推导出最大可能纵向跨距

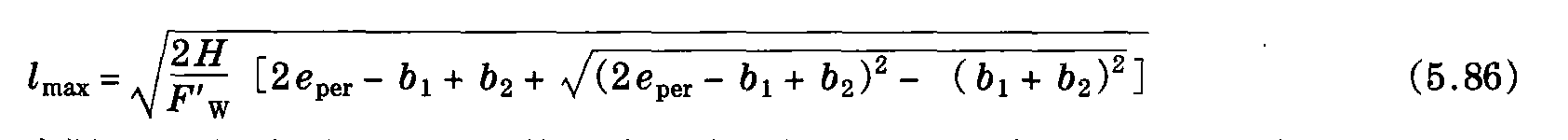
实际上，可以把这个只用于接触线的公式扩展适用到接触悬挂，此时： 用H_OHL＝_HCW+H_CA代替H; F'_WOHL = F'_WCW+F'_WCA，代替F'_W，这个近似值是否可接受取决于接触线和承力索风偏移的比率。如果希望最大允许跨距值计算得更精确些，那么如第5.4.3节所述，就必须考虑承力索和接触线的机械相互作用 (吊弦引起)。

对于尺寸b都相等时，例如b_i＝b₂＝b，就像实际使用的那样，式 (5.86)可简化为

举例： 在德国铁路标准接触网中，当最大速度达200km/h时，可以采用的最大纵向跨距是多少?从图5.18得出位置极限值e_per＝0.55m，从表5.7中查出单位长度的风载为11.5N/m。

承力索和接触线的水平张力均为10kN，对于0.4m的位移值b

在中点锚结附近，张力降低8%，最大跨距即77.1m的悬挂点间距是允许的，如果张力降低11%，最大允许悬挂点间距是75.8m。

如图5.12所示，曲线上最大可能纵向跨距取决于风是从曲线内侧吹还是从外侧吹。实际应用中，只有风从曲线外侧吹才是重要的。如果把e=e_per代入式(5.75)，曲线内最大可能纵向跨距公式是

举例： 在德国铁路的标准架空接触网中，行驶速度最高达200km/h，曲线半径为250m时，可采用的最大纵向跨距是多少?

表5.9包括了德国铁路和法国国铁确定的说明纵向跨距和曲线半径间关系的数值。

表5.9 德国铁路和法国国铁确定的纵向跨距和曲线半径的关系

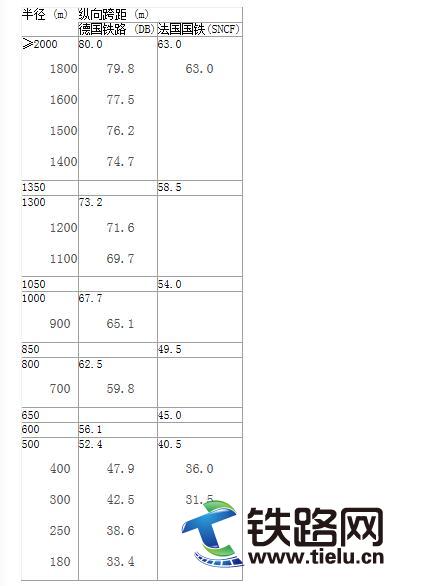
在此计算中，中心锚结处张力降低8%的问题必须予以考虑，例如： 即张力为20kN-1.6kN=18.4kN。根据表5.7，单位长度的风载为11.5N/m。如图5.19，b=0.4m和eper=0.47m时

如果沿曲线相邻悬挂点处的位移值b不相等，则b_i＝b₁，b_i+1＝b₂被应用于图5.12或式 (5.74)，这也能说明，确定最大纵向跨距的公式也适用于接触网系统 [假如式(5.81)和式 (5.82) 置换式适用于这种情况]。下面这个公式，首先在参考文献 [5.5]中阐述，适用于风从曲线外侧吹的情况

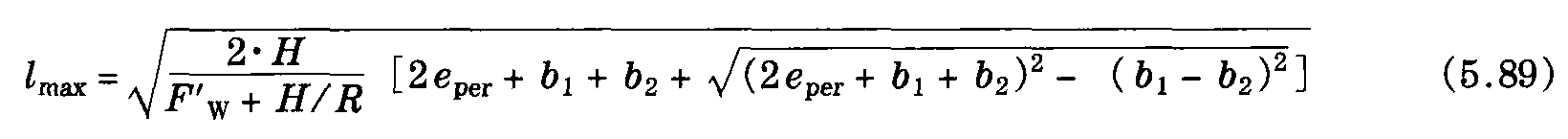
5.5.3 锚段长度的计算

EN 50119标准中称该参数为 “锚段长度” 并且定义为 “两个锚固点之间的导线长度”。通常接触线或接触悬挂是通过大致位于锚段中心锚结点处向两个方向拉出进行补偿的。为了能说明出现的一些物理问题，我们把锚固点和补偿装置之间的区段定为L; 可以认为锚段长度为2L，这就是说，锚结点是在区段的中间部位。