9.2.1 横向冲击沿带张力接触线锚段的传播
确定受电弓和接触网的相互作用的一个标准,就是冲击以波的形式沿接触线锚段传播的方式。将接触线当成没有抗弯刚度而只有张力的一根绳,就可以建立一个具有变化过程的有效模型。将接触线当作易弯曲的梁 [9.3] 是对这种方法的进一步改进。
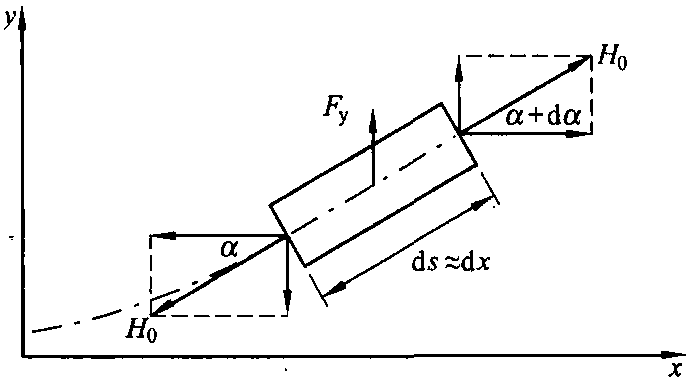
图9.1 作用在接触线单元上力的平衡
为了研究横向冲击的传播,也就是研究受电弓沿接触线锚段移动引起的局部垂直运动。假定接触线纵向应力为σ、密度为γ,其刚度忽略不计 (图9.1)。当一个纵向力H0=σA作用于接触线时,接触线产生横向偏移,根据下列公式,每根线dx长度内均产生一个恢复力
Fy=H0sin(α+dα) -H0sinα≈H0dα(9.1)
在α~tgα=ₔy/ₔx的条件下, 可得出dα≈dx·(ₔ2y/ₔx2)并从中得出一个恢复力
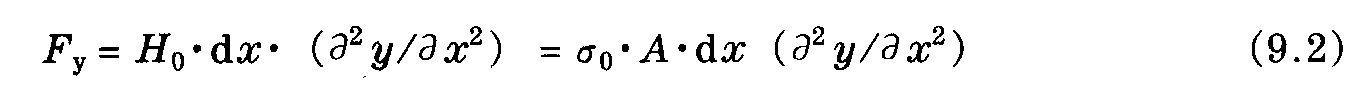
长度dx的线质量是dm=γAdx。 表示长度dx的元素运动方程被转换成
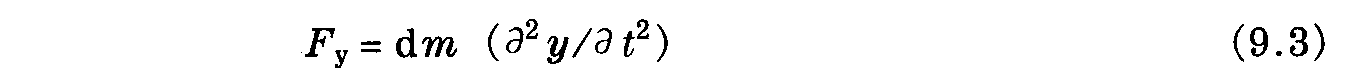
由式 (9.2) 和式 (9.3) 中可推导出带张力接触线的运动方程

该方程在普通力学中表示为张力线或绳索的波动方程。其一般解法是通过含有下列形式的各种函数求出的

其中

cp为波的传播速度。对于张力10kN的Cu AC-100铜线求得数值为![]() 约等于380km/h的速度。
约等于380km/h的速度。
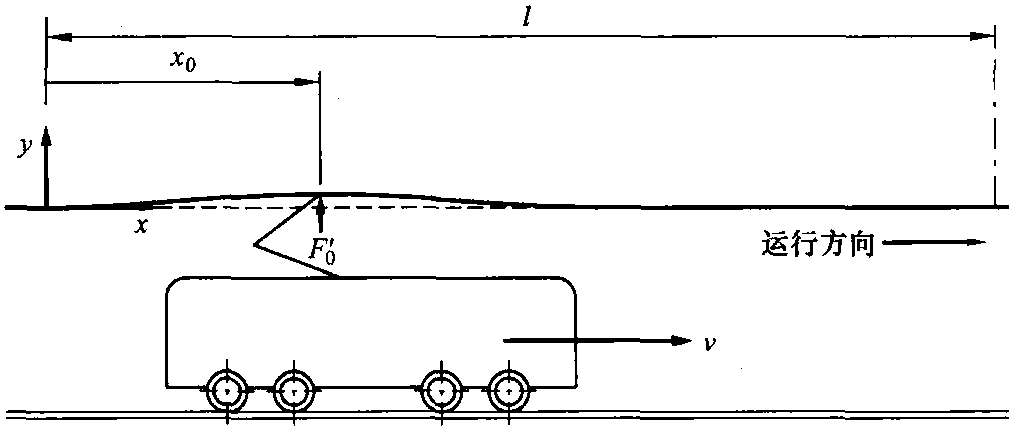
图9.2 带受电弓的车辆沿接触线运行
9.2.2 当一个恒力作用在接触线 (带张力) 的一个点上并沿着该线移动时的接触线特性
为描述当接触线在受电弓以恒力F′0作用于接触线上并按照一定速度v (图9.2) 沿接触线运行时的接触线特性,可以把微分方程式 (9.4) 表示为

如果滑板在时间t=0时,位于点x=0,可用下面公式求出时间t时滑板的位置

在式(9.7) 中,δ(x-x0) 是一个具有δ (0) = 1和δ (x≠0) =0特性迪拉克(Dirac)三角函数。应用已知的边界条件,三角函数可以转换成傅立叶级数

其中

将式 (9.9)和式 (9.10) 代入,式 (9.7) 则变成
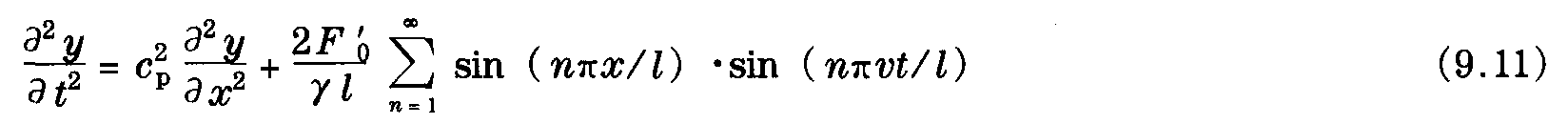
免责声明:本网站所刊载信息,不代表本站观点。所转载内容之原创性、真实性、完整性、及时性本站不作任何保证或承诺,请读者仅作参考并自行核实。