目前岩溶隧道中确定安全岩盘厚度的研究文献很少，而且没有统一的设计理论和方法，如何合理地确定安全距离是个十分复杂的技术难题。通过运用工程地质、水文地质、岩体力学和数值模拟等综合方法，确定安全岩盘厚度与岩体强度、水压力、洞室断面尺寸的关系。

一、安全岩盘厚度工程类比法

安全岩盘厚度与岩体完整程度、水压力、洞室断面尺寸等密切相关，虽然目前国内外尚无统一计算方法，可借用《铁路隧道设计规范》注浆墙允许抗剪强度计算：

d=P·D/(4τ) (6-20)

式中：d、P、D、τ——分别为安全岩盘厚度(m);

P——水压力(MPa);

D——洞室断面等效直径(m);

τ——岩体允许抗剪强度。

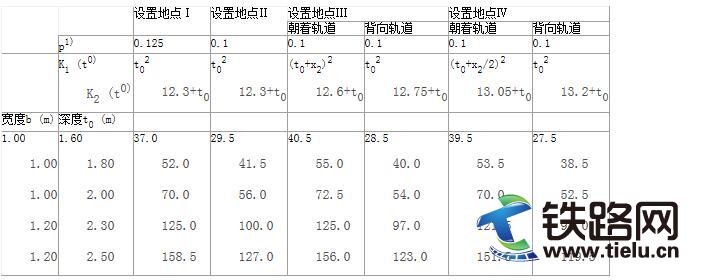
根据《铁路隧道设计规范》(TB10003—2005)Ⅳ级围岩岩体允许抗剪强度为0.72MPa，Ⅱ～Ⅲ级围岩岩体允许抗剪强度为3.80～1.51MPa。隧道正洞断面等效直径为8.7m，经计算得安全岩盘厚度估算表(表6-8)。

表6-8安全岩盘厚度表

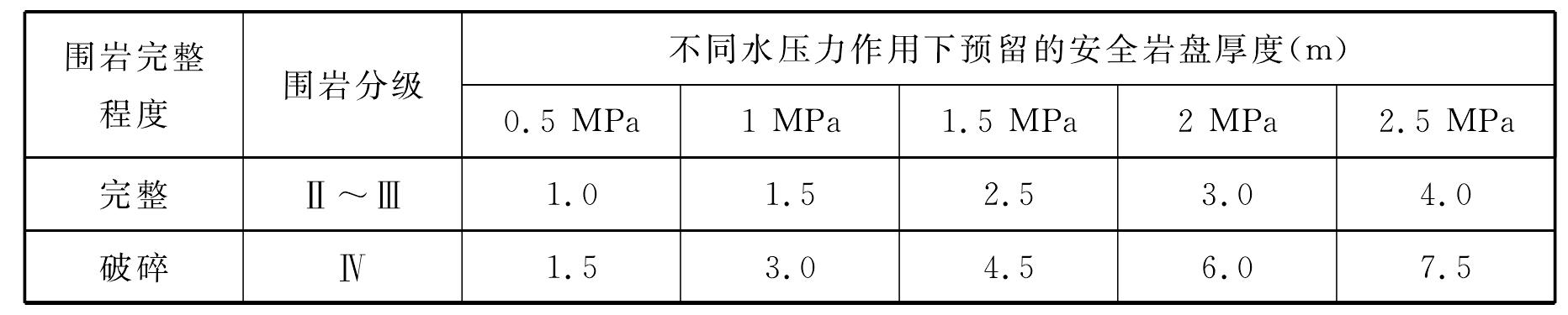
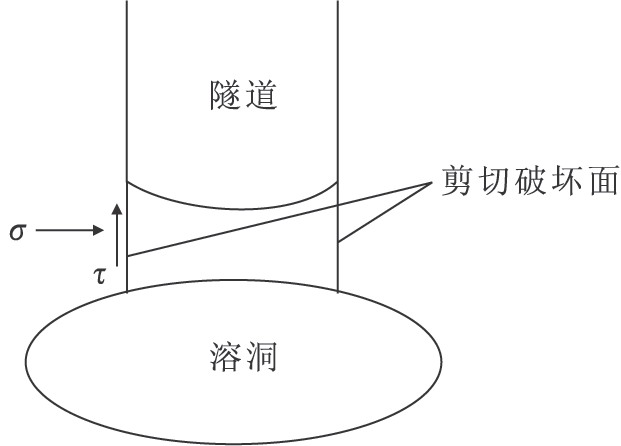
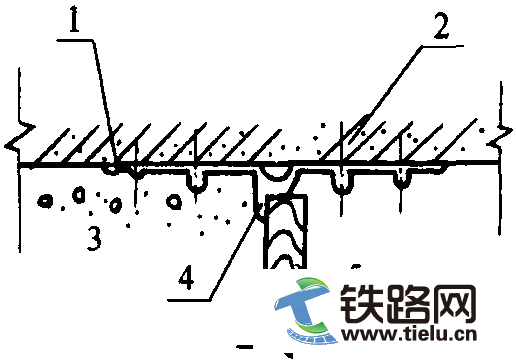
图6-47极限剪切强度公式模型简化平面图

二、安全岩盘厚度极限剪切强度算法

考虑安全岩盘临界失稳时达到其极限抗剪强度，剪切面为隧道断面向溶腔的延伸面(图6-47)，则有：

P×S=[τ]×L×t (6-21)

式中：t——止水岩盘厚度(m);

P——水压力(MPa);

S——开挖断面面积(m2);

τ——岩体抗剪强度(MPa)。

因此，安全岩盘厚度可表示为：

t=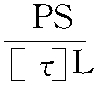(6-22)

在不同的隧道类型和不同的岩体完整程度基础上，用式(6-22)可计算得出不同水压力下的安全岩盘厚度值。

另外，根据莫尔库仑强度理论，岩体的抗剪强度为：

τ=c+σtanφ (6-23)

σ为岩体的正应力，但实际计算中很难简单地得到其值。假定安全岩盘临界失稳时为压剪破坏，而岩盘可视为一厚板，此时将岩盘破坏视为单轴压缩破坏，即此时的岩盘正应力为岩体的单轴抗压强度，因此，采用式(6-23)进行计算时可取σ为岩体单轴抗压强度σm c。

三、安全岩盘厚度椭圆板力学模型算法

如将铁路隧道断面简化为椭圆形，则当隧道与溶腔正交，安全岩盘较薄时，则隧道与溶腔的相互关系可简化为周边固支椭圆板力学模型，如图6-48、图6-49所示。

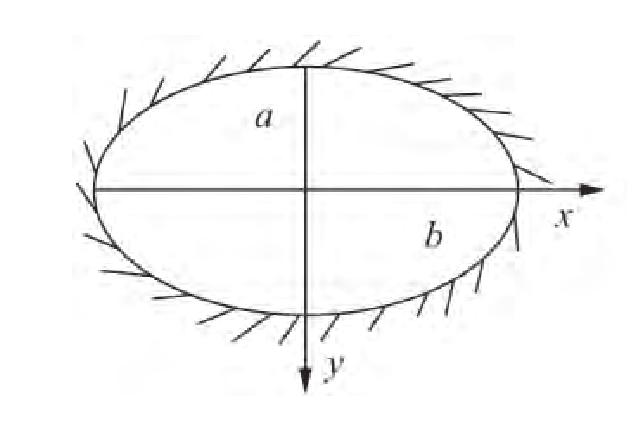
图6-48周边固支椭圆板计算图

图6-49周边固支椭圆板模型剖面示意图

此时，椭圆形安全岩盘受均布荷载。由于结构的复杂性，其应力应变分析很复杂，椭圆板中心处的应力公式的近似解为：

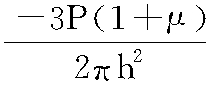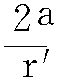σ=(ln-0.317α-0.376)(μ=0.25时) (6-24)

式中：α——短轴与长轴之比，即α=a/b;

P——传递到顶板的总竖向荷载;

r′ ——当量半径，当量半径取决于板厚h，Westergaard提供了当量半径的一个近似计算式：

当r<0.5h时，r′=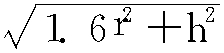-0.675h;

当r>0.5h时，r′=r。

通过以上的分析，当岩盘的边界条件符合周边固定的椭圆板力学模型时，根据荷载状态以及岩体的最大允许拉应力值，即可由公式反推安全岩盘厚度，岩盘厚度近似解为：

h=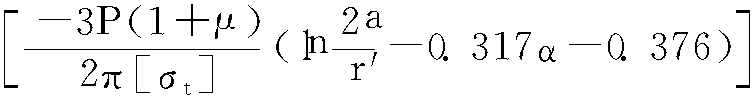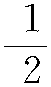(6-25)

四、简化力学模型计算方法对比分析

为对上述各种安全岩盘厚度的计算方法进行综合对比分析，分别对同一隧道不同围岩和溶腔条件下的安全岩盘厚度进行计算，并分析其计算结果。选择BQ岩体分级体系，选取不同岩体级别对应的岩体力学指标。方法①为极限剪切强度计算公式，方法②为椭圆板计算模型。计算结果如表6-9所示。

单纯从计算结果看，可得出以下结论：